|
Курс
лекций Мюнхинского института парапсихологии.
ЛЕКЦИЯ 8
ПРЕДИСЛОВИЕ
Достижение рассмотренной в предыдущей лекции гармонии между человеком
и космосом зависит не только от паранормального духовного развития человека,
но и от пространственно-энергетических космических связей вокруг него.
Ясно, что чем больше имеется доступной свободной пространственной энергии,
тем больше мы можем воспринять посредством наших чакр, тем больше жизненной
энергии мы можем передать нашему материальному телу или излучить в окружающую
среду для осуществления паранормальных воздействий.
Наибольшая часть пространственной энергии земной биосферы — т.е. общее
количество имеющейся в нашем распоряжении пространственной энергии —
поступает от небесных тел нашей Солнечной системы: как любое другое
органическое или неорганическое тело они постоянно излучают посредством
своего Пси-поля пространственную энергию, которая распространяется в
пространстве и в конце концов достигает земной биосферы.
Интенсивность этого излучения не всегда столь постоянна, как хотелось
бы предположить. Она во многом зависит от:
— массы небесного тела;
— его углового положения и его удаления от Земли;
— его углового положения и его удаления от других небесных тел.
Таким образом, количество пространственной энергии, имеющейся в нашем
распоряжении, в первую очередь зависит от положения планет в нашей Солнечной
системе.
Наука астрология уже тысячелетия назад открыла эти связи между излучениями
планет и эмпирически (основываясь на опыте) установила те конфигурации
небесных тел, которые позитивно или негативно влияют на жизнь людей.
Новейшие исследования в области физики (см. лекцию 6) целиком и полностью
подтвердили открытия астрологов.
Мы, как парапсихологи, используем их для определения тех временных моментов,
когда наша паранормальная деятельность "облучается" хорошо
или плохо. Таким образом, в этой лекции мы рассмотрим определение положений
планет, чтобы затем в последующей лекции узнать о воздействии различных
возможных положений планет.
В упражнениях мы продолжаем нашу гармонизацию, которая останется темой
упражнений и в лекции 9.
Обзор истории магии на сей раз выпадает из-за недостатка места в лекции;
в следующей лекции мы займемся магией в Римской империи.
ЗВЕЗДНЫЕ ЧАСЫ
Вместе с восемью другими планетами и многими их естественными спутниками
наша Земля входит в планетарную систему, которая сопровождает Солнце
в его движении по необъятным просторам космоса. Рассеянные с незначительными
отклонениями (Меркурий — 7 градусов, Плутон — 17) на плоскости эклиптики,
которую мы можем представить себе как воображаемый диск, девять планет
вращаются вокруг центральной звезды, Солнца, каждая на своей орбите,
каждая со своей скоростью, каждая на своем расстоянии. Лишь направление
вращения у всех одно.
Силой, удерживающей планеты на их упорядоченных орбитах, является сила
тяжести — гравитация (см. лекцию 1). Вместе с Солнцем 4 большие планеты
— Юпитер, Сатурн, Уран и Нептун — наряду с гравитонами излучают и тепло,
а Солнце еще и кванты света, которые отражаются другими небесными объектами,
не излучающими свет самостоятельно. Земля, Юпитер, Сатурн и Уран обладают
еще магнитным полем, а Юпитер еще и излучает радиоволны.
Вместе с квантами пространстзенной энергии, которые постоянно излучаются
всеми небесными телами пропорционально их массе, эти излучения в своей
совокупности образуют энергетическое поле, через которое движется наша
Земля и интенсивность которого колеблется вместе с изменяющимися положениями
планет.
Выяснение связи этих колебаний и процессов жизни на Земле и является
задачей астрологии. Эта увлекательная наука, которая посредством исследования
положений планет (по астрологической терминологии Солнце и Луна тоже
относятся к планетам) может сделать уверенные предсказания, например,
исходя из момента рождения человека, о его характере и жизненном пути,
является все-таки самостоятельной областью науки, которой мы здесь лишь
коснемся. Нас интересуют только воздействия пространственно-энергетических
излучений планет на наши паранормальные способности.
Они — как мы уже знаем — зависят от трех обстоятельств:
1. Имеющегося в нашем распоряжении объема свободной пространственной
энергии.
2. Свободного излучения модулированной пространственной энергии и
3. Свободного приема пространственно-энергетической информации.
Все три предпосылки тесно связаны с астрономическими положениями планет
внутри нашей Солнечной системы.
Из-за наложения излучаемых энергетическими телами планет пространственно-энергетических
волновых полей они могут усиливаться или ослабляться. Следовательно,
в зависимости от текущего астрономического положения планет в нашей
Солнечной системе, на Землю попадает больше или меньше пространственной
энергии.
Поскольку объем имеющейся в нашем распоряжении пространственной энергии
определяет ее количество, которое мы сможем принять посредством вдыхаемого
воздуха и чакр, чтобы с ее помощью пополнить жизненную энергию нашего
материального тела или предпринять паранормальные воздействия на окружающий
мир, то ясно, что положения планет, в итоге, определяют степень успеха
или неудачи нашей работы.

Рис.1. Масштабное изображение Солнечной системы со временем обращения
планет.
Из-за наложения пространственно-энергетических волновых
полей планет на земные может вдобавок произойти усиление или ослабление
последних, чем также облегчаются или усложняются паранормальные влияния:
мы ведь применяем волны пространственной энергии как носитель-медиум
паранормального обмена информацией или паранормальных влияний на окружающий
мир.
Прежде чем более подробно остановиться на пространственно-энергетически
позитивных или негативных временных моментах и на их определении мы
основательно займемся пространственно-энергетическими связями в нашей
Солнечной системе.
ПЛАНЕТАРНАЯ ПРОСТРАНСТВЕННАЯ ЭНЕРГИЯ
Небесные тела нашей Солнечной системы — как и все другие органические
и неорганические тела — помимо своего вещественного строения обладают
еще и энергетическим телом, которое постоянно излучает пространственную
энергию. Насколько интенсивна та часть излучения, которая в конце концов
достигает поверхности Земли, зависит от следующих факторов:
1. Массы небесного тела,
2. Его углового положения и его удаления от Земли и
3. Его углового положения и его удаления от других небесных тел.
Так как излученная пространственная энергия небесного тела пропорциональна
его массе, то самые большие небесные тела излучают, естественно, наибольшее
количество пространственной энергии. Как, например, Солнце с массой
в 1 971 750x10" кг отдает ровно в 19 143 раза больше пространственной
энергии, чем Нептун с массой
в 102.95x10" кг. А у Плутона с его массой в 0.014x10" кг настолько
незначительное пространственно-энергетическое излучение (1/143500000
солнечного излучения), что его вообще не стоит принимать во внимание;
по этой причине в наших дальнейших расчетах мы Плутон вообще не учитываем.
Рисунок 2 показывает в соответствии с масштабом величины тел Солнечной
системы, а таблица — их массы:
| Солнце |
1 971 750.000x10*24" кг |
Юпитер |
1 899.398x10*24 кг |
| Меркурий |
0.323х102*24 кг |
Сатурн |
568.830x10*24 кг |
| Венера |
4.839x10*24 кг |
Уран |
87.240х10*24 кг |
| Луна |
0.073х10*24 кг |
Нептун |
102.950x10*24 кг |
| Марс |
О.639х10*24 кг |
Плутон |
0.014x10*24 кг |
Какое количество отданного небесным телом излучения в конце концов
достигнет Земли, зависит от его удаления. Пространственно-энергетическое
излучение ведет себя так же, как световое. Вблизи свечи очень светло,
но уже на расстоянии одного или двух метров при чтении нужны усилия,
чтобы различить буквы в книге. При помощи логики выявляется совершенно
простой факт: как световые, так и пространственно-энергетические излучения
равномерно распределяются в пространстве источником излучения. Если
излучение не отклоняется в определенном направлении односторонним экранированием
или фокусировкой, например, при помощи параболического рефлектора, то
оно распространяется в пространстве шарообразно (как круговые волны
на поверхности воды — только в трех измерениях). Так как поверхность
сферы рассчитывается по формуле \~\~AJIR, то излучение с увеличением
удаленности от источника распределяется на все большую площадь и его
интенсивность уменьшается пропорционально квадрату расстояния.

Рис.2. Солнце настолько велико, что все планеты и даже лунная орбита
могли бы поместиться внутри него.

Рис.3. Снижение интенсивности излучения на примере Нептуна.

Рассмотрим это подробнее на примере Нептуна (рис. 3): при радиусе в
50 000 км поверхность планеты составляет 31 400 000 000 км2. Фронт волны,
исходящей из энергетического тела Нептуна пространственной энергии,
уже на расстоянии от поверхности планеты в 50000 км увеличивается в
4 раза, т.е. его поверхность составляет 4x3.14x100000x100000-125600000000
км2), а первоначальная интенсивность излучения снижается в 4 раза. Через
следующие 100000 км, на расстоянии в 150000 км от поверхности Нептуна,
фронт волны распределяется на 502400000000 км2 (4x3.14x200000x200000),
а интенсивность излучения уже составляет только 1/16 часть от первоначального.
Так очень просто объясняется тот факт, что от больших внешних планет
нашей Солнечной системы на Землю поступает гораздо меньше излучения,
чем от сравнительно маленьких небесных тел, расположенных вблизи Земли.
От Луны, например, Земля получает в 32 680 раз больше излучения пространственной
энергии, чем от Нептуна, хотя его масса больше массы Луны в 1396 раз.
Рисунок 4 демонстрирует нам в соответствии с масштабом огромные расстояния
в нашей Солнечной системе:
Поскольку все планеты Солнечной системы обращаются по приблизительно
круговым орбитам вокруг центральной звезды — Солнца, а Земля вращается
довольно близко от него, то можно было бы предположить, что на поверхность
Земли поступает примерно постоянное излучение пространственной энергии,
т.е. как будто постоянно господствуют одинаковые пространственно-энергетические
условия.
То, что это не так, астрология уже в достаточной степени доказала, так
как в этом случае было бы невозможно из времени рождения человека предсказать
по расположениям планет его характер и жизненный путь. Пространственно-энергетические
условия в земной биосфере подвергаются колебаниям, зависящим от расположения
планет.
Причиной этого является свойство различных волновых полей при взаимной
встрече (наложение, интерференция) частично или полностью суммироваться
или угасать.
ЯВЛЕНИЯ ИНТЕРФЕРЕНЦИИ
Повышение (конструктивная интерференция) интенсивности состоящего из
двух или более волновых полей общего волнового поля или его понижение
(деструктивная интерференция) зависит от различных предпосылок: удаленности
источников излучения друг от друга, частоты и амплитуды излучения, интенсивности
излучения волновых полей при встречах друг с другом, а также от того,
встречаются ли друг с другом позитивные или негативные их фазы.
Весь процесс настолько сложен, что лишь немногие физики понимают его
полностью; поэтому мы ограничимся тем, что попытаемся понять его с помощью
двух ярких примеров, в одном из которых происходит удвоение, а в другом
— полное затухание интенсивности излучения: рассмотрим для этого рисунок
5.
То, что волны попеременно проходят вершину (положительная фаза) и впадину
(отрицательная фаза), мы уже знаем из лекции 5. Как вершины волн (а),
так и их впадины (6), исходя из источника излучения, распространяются
в пространстве концентрическими сферическими поверхностями.
Такие трехмерные сферические поверхности, которые имеют одинаковую фазу,
называют фронтами волн. Если встречаются друг с другом два фронта волн
с одинаковой фазой (в), то возникает волновое поле удвоенной интенсивности.
Если же, напротив, встречаются друг с другом два фронта волн, положительной
и отрицательной (г), то они гасят взаимно друг друга — излучение бесследно
исчезает.
В зависимости от фазы интерференция возникает и тогда, когда встречаются
планетарные поля волн. Может случиться так, что мы сможем принимать
информацию при ясновидении из окружающего нас мира в усиленном виде,
в ослабленном виде, а в экстремальном случае — вообще не сможем. Или
же модулированно излучаемая нами пространственная энергия достигнет
объект цели только в ослабленном виде или вообще не достигнет.

Вывод: если у нас возникают проблемы с приемом свободной
пространственной энергии, с внечувственными восприятиями или с паранормальными
воздействиями, то это не следует увязывать с отсутствием паранормальных
способностей — это вполне может зависеть от определенных положений планет!
Поэтому научимся определять углы отклонения планет относительно друг
друга и относительно Земли. Тогда с помощью напечатанной в следующей
лекции таблицы положительных и отрицательных воздействий конфигураций
мы сможем простым способом выяснить, благоприятен ли или нет выбранный
нами момент времени для сложных паранормальных упражнений — таких как
отделение вещественного и энергетического тел или упражнения по телекинезу,
материализации или левитации. Или проверить после их выполнения, основывалась
ли неудача в приеме пространственной энергии или в упражнении только
негативным пространственно-энергетическим положением планет.
ПОЛОЖЕНИЯ ПЛАНЕТ
Для определения угловых положений небесных тел Солнечной
системы относительно друг друга и относительно Земли нам необходимо
знать их точные положения в любой момент времени.
К сожалению, нет сборника таблиц, который содержал бы эти данные на
каждую минуту каждого дня — такой труд был бы, вероятно, более метра
толщиной! Но не пугайтесь: имеются так называемые эфемериды, из которых
мы можем выбрать ежедневные положения небесных тел Солнечной системы
на 0 часов мирового времени (или в полдень, соответствующие данные мы
найдем в начале каждого тома эфемерид).
Исходя из смещений в течение дня мы легко можем рассчитать положения
на любой момент времени.
Пять примеров и пять упражнений для различных моментов времени должны
ознакомить нас с этим процессом. Мы включаем в текст отрывки из "Немецких
эфемерид" для соответствующих моментов времени.
Том VII "Немецких эфемерид" издательства "Отто-Вильгельм-Барт"
охватывает, например, ежедневные положения звезд на период от 1981 до
2000 года.
Прежде чем мы сможем воспользоваться позициями планет, указанными в
эфемеридах, нам нужно еще перевести местное время в всемирное, или время
по Гринвичу (ВГ): все данные эфемерид указаны для этого действительного
для нулевого меридиана времени.
ПРИВЕДЕНИЕ В СООТВЕТСТВИЕ МЕСТНОГО ВРЕМЕНИ С ВРЕМЕНЕМ
ПО ГРИНВИЧУ
можем
ВРЕМЕННЫЕ ПОЯСА
- 11 ч Алеуты, Самоа
-10ч Западная Аляска, Гавайи
- 9ч Восточная Аляска
- 8ч (тихоокеанское время) Западная Канада и западные штаты США (Калифорния),
- 7ч (горное время) части Канады, горные штаты США, Иексика (западная
часть)
- 6ч (центральное время) часть Канады, центральные штаты США, Мексика
(восточная часть)
- 5ч (восточное время) часть Канады, восточная часть США, 1еру, Чили,
Куба
- 4ч (атлантическое время) часть Канады, центральная Бразилия, Парагвай
- Зч (атлантическое время) восточная Бразилия, Гренландия, Аргентина,
Уругвай
- 2ч (атлантическое время) Азорские острова,
- 1 ч (атлантическое время) Исландия, Мадейра
Оч (мировое время по Гринвичу) Великобритания, Ирландия, Испания, Португалия,
Алжир, Морокко
+ 1 ч [среднеевропейское время) Скандинавия, Бельгия, Германия, Польша,
ЧССР
+ 2 ч (восточноевропейское время) Западная часть СССР (Москва), Греция,
Турция, Израиль, Иордания, Египет, ЮАР
+ Зч СССР (Нижний Новгород), Ирак, Мадагаскар, Кения
+ 4ч СССР (Свердловск), Иран
+ 5ч СССР (Омск)
+ 5ч 30 мин Индия, Шри Ланка
+ 6 ч СССР (Новосибирск), Китай [Тибет), Таиланд
+ 7ч СССР (Иркутск), Средний Китай, Вьетнам, Лаос
+ 8ч СССР (Якутск), Корея, Филиппины
<- 9 ч СССР (Комсомольск-на-Аму-ре), Япония, Корея
+ 10ч СССР (Зырянка), восточная Австралия
+ 11 ч СССР (Амбурчик)
+ 11 ч 30 мин Новая Зеландия
Эти временные пояса указаны с наименованиями соответствующих
географических мест. Знак "+" (восточнее Гринвича) или "-"
(западнее Гринвича) указывает на соответствующую разницу поясного времени
относительно мирового. Например, в Западной Германии принято среднеевропейское
время, опережающее гринвичское на 1 час.
В СССР часы дополнительно переставлены на 1 час вперед (отменено 29
сентября 1991 года — прим. ред.). В Великобритании, Испании и Алжире
часы переставлены на 1 час вперед, так что они также показывают среднеевропейское
время.
Особое внимание при расчетах поясного времени следует обращать на вводимое
в определенные времена года летнее время. Поэтому в Германии местное
время с последнего воскресенья марта (2 часов) до последнего воскресенья
сентября (3 часов) соответствует мировому времени, что делает излишним
пересчет местного времени на гринвичское.
КАРТА МИРОВОГО ВРЕМЕНИ
Эта карта делит Землю на 24 различных временных пояса.
Цифры по верхнему краю указывают поясное время, соответствующее 12 часам
по Гринвичу; цифры по нижнему краю обозначают то количество часов, которое
при пересчете местного времени на гринвичское нужно вычесть или прибавить.
Вращение Земли вокруг своей оси обуславливает то, что кульминационный
пункт, т.е. наивысшее положение Солнца, совершает один оборот вокруг
экватора за 24 часа. Поскольку Земля разделена на 360 градусов долготы
(меридианы), каждый час кульминационный пункт сдвигается на 15 градусов.
С тем, чтобы во всех странах полдень наступал примерно тогда, когда
Солнце достигло своего наивысшего положения, Земля была разделена на
24 временных пояса, при этом время в соседних различается на один час
(за исключением Новой Зеландии, Индии, Шри Ланки, имеющих различие в
полчаса), начиная от меридиана отсчета — нулевого меридиана (проходящего
через английское местечко Гринвич).
Поскольку Земля вращается в восточном направлении, а Солнце, как кажется,
перемещается по небу с востока на запад, то в каждом временном поясе,
лежащем восточнее нулевого меридиана, время сдвинуто на час к вечеру,
а в странах, лежащих к западу от нулевого меридиана — на час (или на
1/2 часа) к утру.

Пример: если в Германии по среднеевропейскому времени полдень, то в
Англии часы показывают только 11 часов (по западноевропейскому времени
или по гринвичскому времени), а в Индии уже 17 часов 30 минут.
Таким образом, чтобы перевести местное аремя в гринвичское, мы должны:
— в местах, лежащих к востоку от Гринвича, вычесть из местного времени
по 1 часу на каждый временной пояс, который отделяет данное место от
Гринвича и
— в местах, лежащих к западу от нулевого меридиана, соответственно прибавить
1 час.
— Если результат составляет менее 0 часов, то это означает время предыдущего
дня (Пример: 2 часа 20 минут - 3 часа - предыдущий день: 23ч 20м),
— Соответственно, если результат составляет более 24 часов, то это уже
следующий день (Пример: 23ч Юм + 4ч - следующий день Зч 10м).
Поскольку наши студенты живут и выполняют упражнения практически во
всех странах мира, то мы приводим деление Земли на отдельные временные
пояса. А таблица детально показывает нам, на сколько часов отличается
местное время отдельных государств от мирового времени.
А теперь — к примерам, показывающим нам, как пересчитать местное время
на гринвичское, а также к упражнениям, где мы сами будем производить
такой пересчет:
Пример 1:
Место: Гамбург (Германия)
День: 5 июля 1960
Время: 19ч 20м г
Местное время ........................... 19ч20м
за вычетом различия во времени местное
время - гринвичское время" (-1ч) ........... -01чООм
Время по Гринвичу .......... 5 июля 1960 18ч20м
Пример 2:
Место: Вена (Австрия)
День: 10 октября 1922
Время: Оч 02м
Местное время ........................... 00ч 02м
за вычетом различия во времени "местное
время - гринвичское время" (-1ч) ........... -01ч 00м
Время по Гринвичу.......... 9 октября 1922 23ч 02м
Пример 3:
Место: Питтсбург (США) " День: 30 июня 1948 Время: 19ч 35м
Местное время ........................... 19ч 35м
добавляя разницу во времени "местное
время - гринвичское время" (-5ч) ........... -нЭбч 00м
Время по Гринвичу.......... 1 июля 1948 00ч 35м
Пример 4:
Место: Мельбурн (Австралия)
День: 20 февраля 1940
Время: 7ч
Местное время ........................... 7ч 00м
вычитая разницу во времени "местное время
- гринвичское время" (-10ч) ............... -10ч 00м
Время по Гринвичу ......... 19 февраля 1940 21ч 00м
Пример 5:
Место: Монтевидео (Уругвай)
День: 18 марта 1925
Время: 8ч 20м
Местное время ...........................8ч 20м
прибавляем временную разницу
местное время - гринвичское время" (-Зч) +3ч 00м
Время по Гринвичу ......... 18 марта 1925 11ч 20м
Упражнение 1:
Место: Ганновер (Германия) :
День: 4 апреля 1962
Время: 8ч 40м
Местное время .............................Ч...М
.......... временную разницу "местное время -
гринвичское время" (-...ч)....................Ч...М
Время по Гринвичу ............Ч...М
Упражнение 2:
Место: Гельголанд (Северное море)
День: 2 августа 1911
Время: Оч
Местное время .............Ч...М
.......... временную разницу
гринвичское время" (-...ч) ...Ч...М
Время по Гринвичу .........Ч...М
Упражнение 3:
Место: Инсбрук (Австрия)
День: 30 декабря 1936
Время: 12ч
Местное время ............Ч...М
.......... временную разницу
гринвичское время" (-...ч)....Ч...М
Время по Гринвичу ......
местное время -..Ч...М
Упражнение 4:
Место: Св. Елена (Атлантический океан)
День: 11 апреля 1941
Время: 23ч 08м
Местное время ..........
.......... временную разницу
гринвичское время" (-...ч)....Ч...М
Время по Гринвичу .........Ч...М
'местное время -...Ч...М
Упражнение 5:
Место: Претория (Южная Африка)
День: 13 марта 1936
Время: 17ч 22м
"местное время —...Ч...М
Местное время .........................".. ' ..М..М
.......... временную разницу
гринвичское время" (-...ч)...Ч...М
Время по Гринвичу...Ч...М
После того, как мы рассчитали время для начала упражнения по Гринвичу
(правильные ответы на упражнения даны в следующей лекции), мы можем
определять положения небесных тел Солнечной системы для этого момента
времени.
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ ПЛАНЕТ
Взгляд на ночное небо открывает нам бесчисленное множество звезд различной
яркости. Некоторые из них образуют кажущиеся фигуры, напоминающие нам
земные формы: созвездия.
Большинство из известных сегодня названий 88 созвездий восходит к древнегреческим
мифам. Некоторые из них происходят из еще более древних времен. Та,к
вавилонские астрономы открыли их уже 2000-1000 лет до н.э.
Наиболее известны созвездия, которые видны на плоскости эклиптики "небесного
свода": если мы посмотрим из северного полушария Земли в направлении
орбит планет (и кажущейся орбиты Солнца), то мы сможем увидеть созвездия
Рыб, Овна, Тельца, Близнецов, Рака и Льва, если же смотреть из южного
полушария, то видны созвездия Девы, Весов, Скорпиона, Стрельца, Козерога,
Водолея и — по крайней мере частично — Рыб. Их называют знаками зодиака.
Если смотреть с Земли, то Солнце, Луна и планеты Солнечной системы вращаются
на своих орбитах не далее 16* от плоскости эклиптики. Солнце проходит
зодиак целиком один раз в год, внутренние планеты — несколько раз, а
медленно движущиеся внешние планеты — только частично.
Этот факт 2000 лет назад и побудил астрологов избрать зодиак в качестве
отправного пункта для установления положений небесных тел Солнечной
системы. Они поделили его на 12 равных частей (отрезков) по 30* и назвали
их по наименованиям созвездий.
Началом зодиака (0*) они избрали пункт, в котором Солнце находится 21
марта — в начале весны: в день весеннего равноденствия. От него видимая
солнечная орбита проходила через созвездие Овна, с 21 апреля — Тельца,
с 21 мая — Близнецов и так далее, пока после прохождения через созвездие
Рыб не достигала опять дня весеннего равноденствия.
Сегодня положения знаков зодиака больше не совпадают с теми частями
зодиака, которые выделили древние астрологи, как мы их наблюдаем на
небе. Причиной этого является прецессия (продвижение вперед) Земли.
Земная ось не расположена перпендикулярно плоскости земной орбиты и,
следовательно, эклиптики, а постоянно проделывает юлообразные движения.
Это имеющее период в 25 800 лет (- 1 платонический год) колебание земной
оси ведет к тому, что для одного и того же дня года видимая часть неба
постоянно перемещается.
 Рис 6. Рис 6.
Около 2000 лет назад Солнце в день весеннего равноденствия находилось
в начале созвездия Овна (поэтому и сегодня это место зодиака обозначают
весенним солнцестоянием). Тогда говорили о точке Овна, теперь же точка
весеннего солнцестояния сдвинулась почти к началу созвездия Рыб. Так
что ко дню весеннего равноденствия Солнце входит в созвездие Рыб. А
еще через примерно 2000 лет оно к началу весны достигнет уже Водолея.
Но для астрологической практики и расчета пространственно-энергетических
отношений это смещение не имеет ни малейшего значения: в конце концов
дифференцирующие воздействия на земную биосферу оказывают не удаленные
часто на миллионы световых лет созвездия из неподвижных звезд, входящих
в зодиак, а исключительно только небесные тела нашей собственной Солнечной
системы. А определение их положений с помощью зодиака не зависит от
действительных положений его созвездий.

Рис.7. На этой схеме мы видим положения небесных тел Солнечной системы
15 марта 1982 года на плоскости эклиптики. Пунктиром указаны линии проекции:
Земля — небесное тело — знак зодиака; они отмечают направления взгляда,
на которых мы можем увидеть отдельные небесные тела (и их положение
относительно зодиакальных созвездий)
Рисунок 7 показывает нам сверху действительные положения созвездий
зодиака на плоскости эклиптики по отношению к солнечной орбите; внизу
показаны зодиакальные отрезки, которые мы находим в гороскопе, так,
как они сегодня расположены по отношению к зодиакальным созвездиям.
Какие положения занимают Солнце, Луна и планеты Солнечной системы в
определенные моменты времени в каких зодиакальных отрезках и, следовательно,
в круге гороскопа, мы узнаем из эфемерид. Посмотрим на фрагмент из них,
который относится к июлю 1960 (и, значит, к примеру 1) на рисунке 10.
a) В этом столбце мы находим день месяца, для 0 часов времени (или полдня
— в зависимости от эфемериды) которого действительны указанные в последующих
колонках долготы положения на плоскости эклиптики, если смотреть с Земли
на зодиак) небесных тел Солнечной системы.
b) + с) Все планеты вращаются вокруг Солнца в одном направлении. Наблюдатель,
стоящий к северу от эклиптики, воспринял бы их движение как вращение
против часовой стрелки (поэтому в гороскопе все положения вносятся по
направлению против часовой стрелки).
 Рис.8. Схема
положений планет 15 марта 1982 года в круге гороскопа. Плоскость эклиптики
и зодиакальные отрезки здесь переданы в горизонтальной проекции. Пунктиром
указаны линии проекции: Земля — небесное тело — зодиакальный отрезок. Рис.8. Схема
положений планет 15 марта 1982 года в круге гороскопа. Плоскость эклиптики
и зодиакальные отрезки здесь переданы в горизонтальной проекции. Пунктиром
указаны линии проекции: Земля — небесное тело — зодиакальный отрезок.
Это движение обозначают как правое вращение, а движение в обратном направлении
— как возвратное.
Это различие приобретает значение для рассмотрения мнимого движения
планет. Эти мнимые орбиты, представляющие собой проекцию действительного
движения на небесную сферу, возникают благодаря взаимодействию двух
движений: постоянного смещения пункта наблюдения на Земле и перемещения
самой наблюдаемой планеты.
Кажущаяся орбита планеты может поэтому на какое-то время быть возвратной.
Если планета, находящаяся в оппозиции (на одной прямой с Солнцем и Землей),
обгоняется Землей вследствие большой угловой скорости последней, то
для наблюдателя в проекции получается возвратное движение. То же самое
касается внутренней планеты в нижнем соединении (т.е. когда планета
и Земля находятся на одной и той же стороне Солнца и планета обгоняет
Землю).

Рис 9.
Феномен возвратности легко понять, если представить спортивный автомобиль,
обгоняющий на дороге грузовой автомобиль. И здесь кажется, что грузовик
как бы отступает назад, хотя он и продолжает поступательное движение
в том же направлении, что и спортивный автомобиль.

Рис.10. Фрагмент из Немецких эфемерид, рассчитанный на О часов мирового
времени.
 |
 |
| Рис.11. Возвратное
движение внутренней планеты. |
Рис.12. Возвратное движение внешней
планеты. |
В тех пунктах, где правовращательное движение планет превращается
в возвратное, движение планеты является стационарным.
В эфемеридах временной момент, начиная с которого планета движется возвратно,
обозначается знаком "Ч". Когда движение вновь становится правовращательным,
на это указывает знак "О".
d) В этих четырех столбцах мы видим значения долготы планет Нептун,
Уран. Сатурн и Юпитер.
Поскольку этим внешним планетам для обращения вокруг Солнца необходимо
от 11.9 (Юпитер) до 247 (Сатурн) лет, они лишь на несколько градусов
в году передвигаются в зодиаке. Поэтому мы можем отказаться от точного
до минуты расчета их положений и внести их в круг гороскопа так, как
они указаны для дня упражнения на 0 часов или полдень.
Пример: Нептун 5 июля 1960 находился на б* 25' (б дуговых градусах и
25 дуговых минутах) в зодиакальном отрезке Скорпиона. Значит, на шкале
круга гороскопа мы между 6 и 7 делением (считая, как уже известно, против
часовой стрелки) наносим небольшую черточку, которой мы точно обозначаем
положение планеты, и пишем рядом точную величину градусов. Дополнительно
мы ставим знак R для указания на то, что планета движется возвратно.
С положениями других планет мы поступаем точно так же.

Рис.13.
е) Для Солнца, Луны и для быстрых планет (Марс,
Венера и Меркурий) мы вначале должны взяться за
карандаш и с точностью до минуты рассчитать их
положения, поскольку в течение для они заметно
изменяются. С помощью наших пяти примеров и
упражнений мы изучим этот процесс расчета.
Вначале мы выясним смещение выбранной планеты за
предыдущий день к заданному. Это простой процесс вы-
числений, поскольку мы должны лишь (независимо от того,
рассчитаны ли эфемериды для полудня или для 0 часов
мирового времени) найти разность между положениями
планет на эти дни.
Для планеты Меркурий данное вычисление в нашем примере 1 выглядит так:
Долгота (Longitude, обозначим ее Long),
Меркурия ($) 5.07.60. 040'
Long Меркурия 6.07.60 - 0*01'
Движение в течение одного дня - 0*09'
Экспериментатор, используя эти данные, хочет осуществить упражнение
по телекинезу в 19 часов 20 минут среднеевропейского времени, т.е. в
18 часов 20 минут по Гринвичу. (Время по Гринвичу служит нам в качестве
основы для вычислений, т.к. "Эфемериды" составлены из расчетов
по Гринвичу).
Если "Эфемериды" составлены для О часов мирового времени (отметка
off этом дается на 1-й странице любой таблицы), то мы должны определить
то движение. которое планета совершила за период времени после О часов
(после полуночи). В нашем примере это движение равняется 18 час. 20
мин. Этот отрезок движения планеты мы называем "интервал".
Если "Эфемериды" составлены для 12 часов (для середины дня),
то мы должны для упражнений, производимых во второй половине дня, определить
разницу, начиная с 12-ти часов, а также соответствующее движение планеты
в этот отрезок времени. Для упражнений, производимых в первой половине
дня, мы определяем разницу до 12-ти часов, а затем — исходя из этого
-— интервал.
Для этой цели в "таблице пропорциональных логарифмов", которая
напечатана в любой книге "Эфемерид" и которая приложена также
к данной лекции, мы находим логарифм (сокращенно Log) движения планеты
в течение суток. (Для нашего примера — логарифм движения Меркурия в
течение суток, равного 0*09'). Кроме того, мы выписываем разницу во
времени (в нашем примере — 18 час. 20 мин.)
Внимательно посмотрим на рис. 14, где наглядно показано, как производятся
описанные действия.
Оба выписанных значения мы складываем и получаем в качестве результата
логарифм ("Log") движения планеты в интервале. (То есть для
нашего примера логарифм движения, которое совершила планета Меркурий
5-го июля 1960 года в течение отрезка времени, равного 18 час. 20 мин.).
Для нашего примера это вычисление выглядит так:
Log 0*09' 2.2041
прибавить Log 18 час. 20 мин. + .1170
Log движения $ за 18 час. 20 мин. -2.3211
Вычисленное таким способом Log-движение мы должны снова преобразовать
в географическое движение, чтобы можно было вычислить позиции планеты
в интересующий нас момент. Это можно сделать также при помощи нашей
"таблицы логарифмов", в которой теперь мы должны отыскать
число, самое близкое по значению к найденному нами Log-числу.

Рис.14.

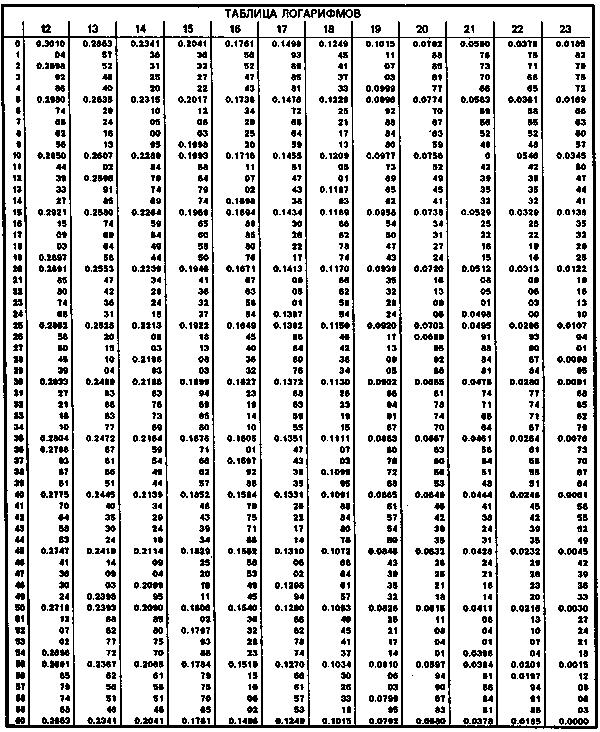
Таким числом будет число 2.3133. Посмотрим в графе "часы или
градусы" нашей таблицы и получим значение 0*. а в графе "минуты"
мы получаем значение 7 минут. Итак, мы получили движение планеты, в
нашем примере — планеты Меркурия, в течение 18 час. 20 мин., равное
О.'ОТ (Это движение мы и будем далее называть интервалом).
Теперь нам остается только прибавить полученный интервал к указанному
в "Эфемеридах" значению позиции планеты или вычесть интервал
из этого значения:
Если "Эфемериды" составлены для 0 часов мирового времени (например,
как в используемых нами "Немецких эфемеридах", начиная с III
тома), то мы поступаем следующим образом:
Если планета, позицию которой для данного момента мы хотим определить,
совершает обратное движение, (как в нашем примере это происходит с Меркурием,
начиная с 4-го июля,— см. значок "ВТ/ то мы отнимаем интервал от
позиции планеты в указанный день в О часов.
Если же планета, наоборот, движется вперед (как в нашем примере это
опять происходит с Меркурием, начиная с 29-го июля,— см. значок "D"},
то мы прибавляем интервал к позиции планеты в полночь (в О часов).
Если же "Эфемериды" составлены, наоборот, для 12-ти часов
дня ("Немецкие эфемериды", тома 1-й и II-й), мы определяем
позицию на момент рождения следующим образом:
Если планета находится в обратном движении, для момента в первой половине
дня мы прибавляем интервал к позиции в полдень, а для момента во второй
половине дня мы отнимаем интервал от позиции в полдень.
Если же планета движется вперед, для первой половины дня мы отнимаем
интервал от позиции в полдень, а для второй половины дня прибавляем
его к позиции в полдень.
В нашем примере это выглядит следующим образом:
Long-позиция 5.07.60 в 0 час. 0'10'
вычитаем интервал (движение за 18 ч. 20 мин.) - 0'07'
Позиция на момент упражнения - 0'03'
Эту позицию мы заносим в наш формуляр гороскопа, а затем повторяем
все проделанные действия для каждой из всех быстрых планет. В наших
примерах мы хотим отразить этот процесс подробно и последовательно.
Но вначале выучим наизусть и запомним знаки, обозначающие планеты:
Солнце
Земля
Луна
Меркурий
Венера
Марс
Юпитер
Сатурн
Уран
Нептун
Плутон
Плутон мы привели здесь только для полноты изложения. Его влияние
в астрологическом аспекте является спорным и не подтверждено ни опытными
данными, ни научными исследованиями. В используемых нами "Эфемеридах"
его позиции также на указываются. Поэтому мы не принимаем эту планету
во внимание при нашей дальнейшей работе.
ПРИМЕР 1
Сначала мы определяем позиции медленных планет:
Нептун - 06*25' — обратное движение
Уран ф - 19*02'
Сатурн - 15*17' — обратное движение
Юпитер - 26*53' — обратное движение.
Эти позиции долготы мы заносим в наш формуляр гороскопа без изменений
(без дополнительных расчетов), поскольку соответствующие планеты в течение
одного дня едва заметно изменяют свою позицию.
(См. таблицу 1, все значения которой относятся к 0 час. мирового времени).
Перейдем к вычислению позиций быстрых планет на момент упражнения. Прежде
всего нам необходимо узнать Log-значение разницы между временем рождения
и значением, указанным в "Эфемеридах", т.к. это Log-значение
нам понадобится во всех вычислениях.
Поскольку нас интересуют 18 час. 20 мин. гринвичского времени, и наши
"Эфемериды" составлены для 0 часов мирового времени, получается
разница во времени, равная 18 час. 20 мин. Log-значение этой разницы
мы выписываем из "таблицы логарифмов": 1170. Теперь мы можем
начинать вычисление позиций отдельных планет:
Солнце:
Long 6 июля 1960 года 13*55'09"
Long 5 июля 1960 года - 12*57'58"
Движение за день - 00*5741"
Log 00'57'(11') 1.4025
прибавим Log 18 час. 20мин. + .1170
Log-значение интервала -1.5195
Интервал - 0*44'
Позиция О 5.07. в 00 час. 12*57'58"
прибавим интервал + ОО'44'ОО"
Позиция О в начале упражнения - 13*41*58"
Луна:
Long 6.07.60. 03*52'
Long 5.07.60 - 19*16' ГЛ.
Движение в течение дня - 14*36'
Log от 14-36' .2159
прибавим Log 18 час. 20 мин. + .1170
Log-значение интервала - .3329
Интервал - 11*09'
Позиция 3) 5.07. в 00 час. 19*16'
прибавим интервал + 11*09*
Позиция луны на момент начала упражнения - 00*25'

Таблица 1.
Меркурий:
Позицию Меркурия мы уже вычислили выше: 0*03'
Венера:
Long 6.07.60 ....17*36'
Long 5.07.60......-16*22'
Движение в день упражнения -01*14'
Log от 01*14' ....................1.2891
прибавим Log 18 час. 20 мин.+ .1170
Log-значение интервала - 1.4061
Интервал - 00*57'
Позиция венеры 5.07. в 00 час. ...... 16*22'
прибавим интервал + 00*57'
Позиция на момент начала упражнения - 17'19'

Рис.15. Формуляр гороскопа для примера 1.
Марс:
Long 6.07.60 11'16
Long 5.07.60 - 10*33'
Движение в день упражнения - 00*43'
Log от 0*43' 1.5249
прибавим Log 18 час. 20 мин. + .1170
Log-значение интервала -1.6419
Интервал - 0*33'
Позиция марса 5.07 в 0 час. 10*33' б
прибавим интервал + 00*33'
Позиция марса на момент начала упражнения - 11*06'
Вычисленные позиции заносим в формуляр гороскопа:

Таблица 2.
ПРИМЕР 2 (см. таблицу 2 и гороскоп ниже)
Позиции медленных планет:
Нептун - 11'41
Уран - 10*21' — обратное движение
Сатурн - 11*16'
Юпитер - 26*15'
(См. таблицу, все значения которой действительны для 12 часов дня по
Гринвичу).
Упражнение намечено на 10 октября 1922 года в О час. 02 мин. среднеевропейского
времени, то есть, 9 октября 1922 года в 23 час. 02 мин. по Гринвичу.
Поэтому для нас решающими являются данные таблицы в графе "9 октября".

Рис.16. Формуляр гороскопа для примера 2.
Поскольку "Эфемериды" составлены для 12-ти часов дня, получается
разница, равная 11 час. 02 мин. Log-значение этой разницы мы определяем
по "таблице логарифмов": 3375. Теперь мы можем перейти к вычислению
позиций быстрых планет.
Солнце:
Long 10.10.22 16^3'36"
Long 9.10.22 - 15*24'18"
Движение в течение дня упражнения - 0*59' 18"
Log от 0'59' (18")1.3875
прибавим Log от 11 час. 02 мин.+ .3375
Log-значение интервала-1.7250
Интервал- 0-27'
Позиция солнца 9.10 в 12 час. 15'24'18"
прибавляем интервал + 0*27'00"
Позиция солнца на момент начала упражнения - 15*51'18"
Луна:
Long 10.10.22 05*48'
Long 09.10.22 - 23*29'
Движение в течение дня упражнения - 12*19'
Log от 12*19' .2879
Log от 11 час. 02 мин. + .3375
Log-значение интервала - .6272
Интервал - 5*40'
Позиция 9.10. в 12 час. 23*29'
прибавляем интервал + 05*40'
Позиция I на момент начала упражнения - 29*09'
Меркурий:
Long 9-го октября 1922г. 27*43'
Long 10-го октября 1922г.- 26*51'
Движение в течение дня упражнения- 0*52'
Log от 0*52'1.4424
прибавляем Log от 11 час. 02 мин.+ .3375
Log-значение интервала-1.7799
Интервал- 0*24'
Позиция венеры 9 октября в 12 час.27*43'
вычитаем интервал- 0*24'
Позиция венеры на момент начала упражнения - 27*19'
Венера: Q
Long 10-го октября 1922г. 29*42'
Long 09-го октября 1922г. - 28*59'
Движение в течение дня упражнения - 0*43'
Log от 0*43' 1.5249
Log от 11 час. 02 мин. прибавляем + .3375
Log-значение интервала - 1.8624
Интервал - 0*20'
Позиция венеры 9 октября в 12 час. 28*59'
прибавляем интервал + 0*20'
Позиция венеры на момент начала упражнения - 29*19'
Марс:
Long 10-го октября 1922г. 16*19'
Long 9 октября 1922г. - 15*40'
Движение в течение дня упражнения - 0*39'
Log от 0*39' 1.5673
прибавляем Log от 11 час. 02 мин. + .3375
Log-значение интервала -1.9048
Интервал - 0*18'
Позиция марса 9 октября в 12 час. 15*40' г
прибавляем интервал + 0*18'
Позиция марса на момент начала упражнения - 15*58'
Вычисленные значения мы заносим в формуляр гороскопа.
В этом примере нужно обратить внимание на то, что Меркурий совершает
обратное движение, поэтому мы должны вычесть интервал из позиции в 12
часов дня.
ПРИМЕР 3 (См. таблицу 3, все значения для 0 час. мирового времени,
и гороскоп рис.17)
Позиции медленных планет:
Нептун -10'14'
Уран - 27*06'
Сатурн - 20*13'
Юпитер- 22*07
Начало упражнения произошло 30 июля 1948 года в 19 час. 35 мин. в Питтсбурге
(США). По Гринвичу в этот момент уже было 1 июля, 0 час. 35 мин.
Из этого получается разница во времени, равная 35 мин., Log-значение
этой разницы: 1.6143. Теперь мы можем вычислить позиции быстрых планет.
Солнце:
Long 2 июля 1948 года 10*00'13"
Long 1 июля 1948 года - 09'03'О1
Движение в течение дня упражнения - 0*57'12"
Log от 0*57' (12") 1.4025
прибавляем Log от 35 мин. + 1.6143
Log-значение интервала -3.0168
Интервал - 0*01'
Позиция солнца на 0 час. 1-го июля 09'03'01
прибавляем интервал + 0*01'00"
Позиция солнца на момент начала упражнения - 09'04'01
Луна:
Long 2-го июля 1948 г. 07*04'
Long 1-го июля 1948 г. - 24*26'
Движение в течение дня упражнения - 12*38'
Log от 12*38' .2787
прибавим Log от 35 мин. + 1.6143
Log-значение интервала -1.8930
Интервал - 0*18'
Позиция луны на 0 час. 1 июля - 24*26'
прибавим интервал + 0*18'
Позиция луны на момент рождения - 24*44*
Меркурий, Венера, Марс:
Поскольку позиции этих планет в течение 35 минут сдвигаются лишь на
несколько секунд, мы можем

Таблица 3.
соответствующие данные перенести в формуляр гороскопа непосредственно
из "Эфемерид".
Меркурий - 29*06' П, обратное движение R.
Венера - ?.9*04' П, обратный ход ft.
Марс
- 20*52' (TV-
Полученные данные мы найдем уже записанными в формуляр гороскопа.

Рис.17. Формуляр гороскопа для примера 3.
ПРИМЕР 4 (см. таблицу 4 и гороскоп ниже)
Начало упражнения произошло в Мельбурне в 7 часов. Поскольку Мельбурн
расположен на 10 час. восточнее Гринвича, мы должны вычесть этот отрезок
времени, тогда мы получим время упражнения по Гринвичу: 21 час по Гринвичу
19 февраля 1940 года.
Вначале мы снова определим позиции медленных планет:
Нептун - 24'49'
Уран - 18'13'
Сатурн - 26'52'
Юпитер- 09'ЗЗ'
Поскольку "Эфемериды" составлены для 0 часов мирового времени,
получается разница в 21 час. Log-значение этой разницы составляет: 580.
Теперь мы можем перейти к определению позиций быстрых планет.
(См. таблицу 4, все значения которой действительны для 0 час. мирового
времени).
Солнце:
Long 20 февраля 1940 года 0' 12'25"
Long 19 февраля 1940 года - 29'11'56"
Движение в течение дня упражнения - 01'00'29"

Таблица 4.
Log от Г (0'29") прибавим 1.3802
Log от 21 час. + . 580
Log-значение интервала -1.4382
Интервал- 0*56'
Позиция солнца на 0 час. 19 февраля 29'11'56"
прибавляем интервал + 0*53'00"
Позиция солнца на момент начала упражнения - 0*04'53"
Луна:
Long 20 февраля 1940 г.12*56'
Long 19 февраля 1940 г. - 28*59'
Движение в течение дня упражнения - 13*57'
Log от 13*57'- .2356
прибавляем Log от 21 час. + . 580
Log-значение интервала - .2936
Интервал - 12*12'
Позиция луны на 0 час. 19 февраля 28*59'
прибавляем интервал + 12*12'
Позиция луны на момент начала упражнения - 11*11'

Рис.18. Формуляр гороскопа для примера 4.
Меркурий:
Long 20 февраля 1940 г. 15*00'
Long 19 февраля 1940 г. - 13*18'
Движение в течение дня упражнения - 1*42'
Log от 01*42' 1.1498
прибавляем Log от 21 час. + . 580
Log-значение интервала -1.2078
Интервал - 1*29'
Позиция меркурия на 0 час. 19 февраля 13*18'
прибавляем интервал + 1*29'
Позиция меркурия на момент начала упражнения - 14*47'
Венера:
Long 20 февраля 1940 г. 9*16'
Long 19 февраля 1940 г. - 8*05'
Движение в течени^ дня упражнения - 1*11'

Таблица 5.
Log от 01*11' 1.3071
прибавляем Log от 21 час. + . 580
Log-значение интервала - 1.3651
Интервал - 1*02'
Позиция венеры на 0 час. 19 февраля 08*05'
прибавляем интервал + 01*02'
Позиция венеры на момент начала упражнения - 09*07'
Марс:
Long 20 февраля 1940 г. 1'58'
Long 19 февраля 1940 г. 1'18'
Движение в течение дня упражнения - 0*40'
Log от 40 мин. 1.5563
Log от 21 час. прибавляем + . 580
Log-значение интервала -1.6143
Интервал - 35'
Позиция марса на 0 час. 19 февраля 1*18'
прибавляем интервал + 0*35'
Позиция марса на момент начала упражнения - 1*53'
Полученные данные мы заносим в формуляр гороскопа.
ПРИМЕР 5
Поскольку упражнение намечено на 18 марта 1925 года в 8 час. 20 мин.
в Монтевидео, получается, что это 11 час. 20 мин. по Гринвичу.

Рис.19. Формуляр гороскопа для примера 5.
Позиции медленных планет:
Нептун - 20'17'
Уран - 2Г48'
Сатурн - 13'49'
Юпитер - 18*24'
(См. таблицу 5, все значения которой действительны для 12 часов дня
по Гринвичу).
Поскольку наши "Эфемериды" составлены для 12 часов дня гринвичского
времени, в этом случае получается разница в 40 мин. между началом упражнения
и временем,

Таблица 6. Все значения даны для О ч мирового времени.

Таблица 7. Все значения даны для 12 ч мирового времени.

Таблица 8. Все значения даны для О ч мирового времени.

Таблица 9. Все значения даны для О ч мирового времени.
для которого вычислены позиции планет. Как и в примере 3, здесь мы
вычисляем только точные позиции Солнца и Луны, так как все остальные
быстрые планеты в течение 40 мин. продвигаются лишь на несколько секунд.
Сначала мы, как и прежде, найдем Log-значение 40 мин., которое составляет
1.5563, а затем примемся за вычисления.
Солнце:
Long 18 марта 1925 г. 27*22'59"
Long 17 марта 1925 г. - 26*23'19"
Движение в течение дня упражнения - 0*59'40"
Log от 59' (40") 1.3802
прибавляем Log от 40 мин. + 1.5563
Log-значение интервала -2.9365
Интервал - 2'
Позиция солнца на 12 час. 18 марта 27*22'59"
вычитаем интервал - 0'02'00"
Позиция солнца на момент начала упражнения - 2Г20'59"
Луна:
Long 18 марта 1925 г. 07*36'
Long 17 марта 1925 г. - 23*28'
Движение в течение дня упражнения - 14*08'
Log от 14*08' (40") .2300
прибавляем Log от 40 мин. + 1.5563
Log-значение интервала -1.7863
Интервал - 24'
Позиция луны на 12 час. 18 марта 07*36'
вычитаем интервал 0*24'
Позиция луны на момент начала упражнения - 07*12'
Меркурий, Венера, Марс:
Меркурий - 9*41'
Венера - 18* 3'
Марс - 26*27'
Таким образом, мы определили позиции планет для нашего последнего примера.
Эти значения мы заносим в формуляр гороскопа. (См. гороскоп 10).
Упражнения 1-5:
Для пяти упражнений мы сами определим положения небесных тел Солнечной
системы с помощью приведенных в таблицах 6-9 фрагментов из эфемерид
и внесем их в круги гороскопа, прилагаемые к лекции.
Для контроля мы найдем в следующей лекции, в которой мы будем определять
также угловые положения, правильно заполненные круги гороскопа.
|






 Рис 6.
Рис 6.
 Рис.8. Схема
положений планет 15 марта 1982 года в круге гороскопа. Плоскость эклиптики
и зодиакальные отрезки здесь переданы в горизонтальной проекции. Пунктиром
указаны линии проекции: Земля — небесное тело — зодиакальный отрезок.
Рис.8. Схема
положений планет 15 марта 1982 года в круге гороскопа. Плоскость эклиптики
и зодиакальные отрезки здесь переданы в горизонтальной проекции. Пунктиром
указаны линии проекции: Земля — небесное тело — зодиакальный отрезок.




















